Chapter 9: Beyond Money - Budgets and Barter
In classical Game Theory, we assume Quasi-Linear Utility:
This assumes you can always pay. But what if you have a Budget Constraint ()?
If Payment > Budget: Utility drops to (Bankruptcy).
Part 1: The Clinching Auction¶
Imagine selling identical items (like ad clicks) to bidders with strict daily budgets.
Standard Ascending Auction: Fails. If prices rise, a high-value bidder might suddenly go broke and drop to demand 0, crashing the price.
The Solution: The Clinching Auction.
We raise the price gradually.
Instead of asking “Who is left?”, we ask “Is the supply so low that you are guaranteed to win?”
If the total demand of everyone else is less than the supply, you mathematically “clinch” the leftover items.
Part 2: Mechanism Design Without Money (Barter)¶
What if we can’t use money at all? The Scenario: 4 Students have been assigned dorm rooms. They are unhappy. They want to swap.
Problem: Agent A wants B’s room. Agent B wants C’s room. Agent C wants A’s room.
Solution: The Top Trading Cycle Algorithm (TTCA).
Everyone points to their favorite room.
This creates a directed graph.
There is guaranteed to be at least one Cycle.
Agents in the cycle swap houses and leave the game.
Let’s visualize the “Pointing Graph” for the dormitory problem.
import matplotlib.pyplot as plt
import networkx as nx
def visualize_ttca_cycle():
"""
Visualizes one step of the Top Trading Cycle Algorithm.
Scenario: 4 Students want to swap dorm rooms.
"""
# 1. Setup Agents and their Current Houses
# Agent 1 has House 1, wants House 2
# Agent 2 has House 2, wants House 3
# Agent 3 has House 3, wants House 1
# Agent 4 has House 4, wants House 2 (But 2 is busy in a cycle)
G = nx.DiGraph()
# Add Nodes (Students/Houses)
G.add_nodes_from([1, 2, 3, 4])
# Add Edges (Preferences)
# Edge i -> j means "Student i points to Student j's house"
edges = [
(1, 2), # Student 1 wants House 2
(2, 3), # Student 2 wants House 3
(3, 1), # Student 3 wants House 1 (CYCLE FORMED!)
(4, 2) # Student 4 wants House 2 (No cycle for 4 yet)
]
G.add_edges_from(edges)
# 2. Detect Cycles
try:
cycles = list(nx.simple_cycles(G))
# Filter for the main cycle [1, 2, 3]
main_cycle = [c for c in cycles if len(c) > 1][0]
except IndexError:
main_cycle = []
# 3. Visualization
pos = {
1: (0, 1), # Top Left
2: (1, 1), # Top Right
3: (1, 0), # Bottom Right
4: (0, 0) # Bottom Left
}
plt.figure(figsize=(8, 6))
# Draw all nodes and edges
nx.draw_networkx_nodes(G, pos, node_size=2000, node_color='lightgray', edgecolors='black')
nx.draw_networkx_labels(G, pos, font_size=16, font_weight='bold')
nx.draw_networkx_edges(G, pos, arrowstyle='->', arrowsize=20, width=2, edge_color='gray')
# Highlight the Cycle
if main_cycle:
# Create list of cycle edges: (1,2), (2,3), (3,1)
cycle_edges = []
for i in range(len(main_cycle)):
u = main_cycle[i]
v = main_cycle[(i + 1) % len(main_cycle)]
cycle_edges.append((u, v))
nx.draw_networkx_edges(G, pos, edgelist=cycle_edges, edge_color='green', width=4, arrowsize=30)
nx.draw_networkx_nodes(G, pos, nodelist=main_cycle, node_color='lightgreen', edgecolors='green')
plt.title("Top Trading Cycle Algorithm: Finding the Trade", fontsize=15)
plt.text(0.5, -0.2, "Green Path = A Valid Trade Cycle found!\nStudent 1, 2, and 3 swap rooms among themselves.\nStudent 4 is left waiting.",
ha='center', fontsize=12, bbox=dict(facecolor='white', alpha=0.5))
plt.axis('off')
plt.show()
visualize_ttca_cycle()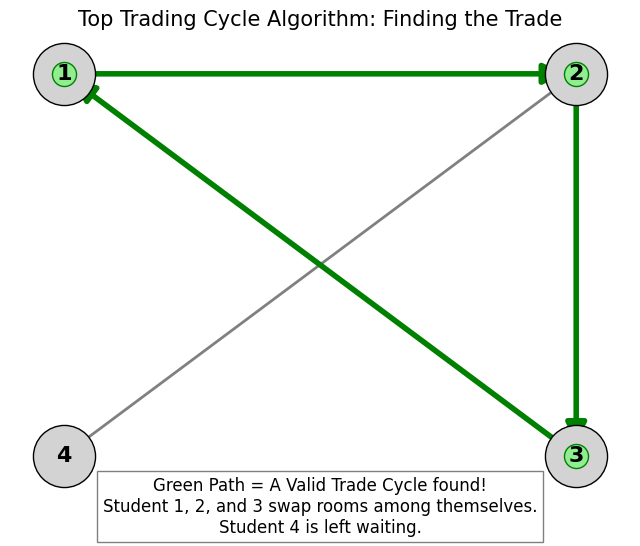
Now, let’s look at the Clinching Auction for Budgeted Bidders.
Scenario: Selling 100 Ad Clicks.
Bidder A: Values clicks at $5, Budget $20. (Can buy max 4 clicks).
Bidder B: Values clicks at $3, Budget $50.
Logic: As price goes up, buyers can afford fewer items. If Bidder B’s demand drops, Bidder A “clinches” the items B can no longer afford.
import math
def run_clinching_auction():
# Setup
TOTAL_ITEMS = 10
# Format: {'name': Name, 'val': ValuePerItem, 'budget': TotalBudget}
bidders = [
{'id': 'A', 'v': 10, 'B': 20, 'won': 0}, # Rich valuation, poor budget (Max 2 items)
{'id': 'B', 'v': 4, 'B': 40, 'won': 0}, # Low valuation, rich budget (Max 10 items)
]
supply = TOTAL_ITEMS
price = 0.0
price_increment = 0.5
print(f"--- Clinching Auction (Items: {TOTAL_ITEMS}) ---")
# Run Auction Loop (Price rises from 0 to max valuation)
while supply > 0 and price < 12:
price += price_increment
# 1. Calculate Current Demand for everyone
demands = {}
for b in bidders:
if price > b['v']:
d = 0 # Price too high
elif price == 0:
d = 999 # Infinite demand at 0
else:
# Demand limited by Budget
max_affordable = math.floor(b['B'] / price)
# Demand limited by Supply + Won (Can't want more than exists)
d = min(max_affordable, TOTAL_ITEMS)
demands[b['id']] = d
# 2. Check for Clinching
# You clinch if Supply > Sum of Others' Demand
for b in bidders:
others_demand = sum([demands[o['id']] for o in bidders if o['id'] != b['id']])
# Available for me = Supply - Others
# Actually, in strict clinching, we look at residual supply.
# Simplified: If Others want 8, and Supply is 10, I am GUARANTEED 2.
guaranteed = max(0, TOTAL_ITEMS - others_demand)
newly_clinched = guaranteed - b['won']
if newly_clinched > 0:
# We can only clinch what is currently available
amount = min(newly_clinched, supply)
if amount > 0:
b['won'] += amount
b['B'] -= amount * price # Pay from budget
supply -= amount
print(f"Price ${price}: Bidder {b['id']} CLINCHES {amount} items! (Rem Supply: {supply})")
print("-" * 30)
print("Final Results:")
for b in bidders:
print(f"Bidder {b['id']}: Won {b['won']} items. Remaining Budget: ${b['B']:.2f}")
run_clinching_auction()--- Clinching Auction (Items: 10) ---
Price $2.5: Bidder B CLINCHES 2 items! (Rem Supply: 8)
Price $3.0: Bidder B CLINCHES 2 items! (Rem Supply: 6)
Price $3.5: Bidder A CLINCHES 2 items! (Rem Supply: 4)
Price $3.5: Bidder B CLINCHES 1 items! (Rem Supply: 3)
Price $4.0: Bidder A CLINCHES 2 items! (Rem Supply: 1)
Price $4.0: Bidder B CLINCHES 1 items! (Rem Supply: 0)
------------------------------
Final Results:
Bidder A: Won 4 items. Remaining Budget: $5.00
Bidder B: Won 6 items. Remaining Budget: $21.50
Analysis of the Clinching Auction¶
In the simulation, you should see something counter-intuitive:
Bidder A (High Value $10) has a small budget ($20). They can afford at most 2 items.
Bidder B (Low Value $4) has a huge budget.
As the price rises to $4, Bidder B’s demand stays high (they can afford plenty). Bidder A cannot “clinch” anything because B wants them all. But once the price crosses $4, Bidder B drops out (Price > Value).
Suddenly, Bidder B’s demand goes to 0.
Bidder A instantly clinches the remaining items (up to their budget limit).
This mechanism ensures fairness. Bidder A gets items only when they are “uncontested” or when the competitor drops out, and they pay the price at the specific moment the item was secured.