Chapter 2: Mechanism Design - The Art of Letting People Be Selfish
In Chapter 1, we saw how selfish behavior causes traffic jams. In this chapter, we ask the reverse question: Can we design a system where selfish behavior actually leads to the best possible outcome?
This field is called Mechanism Design (often called “Reverse Game Theory”). Instead of analyzing a game, we build the game rules so that players, acting in their own self-interest, unintentionally solve a problem for us.
The Problem: Selling a Single Item¶
Imagine you are selling a slightly used smartphone. You have potential buyers.
Each buyer has a private valuation (): the maximum amount they are willing to pay. You don’t know this number.
You want to give the phone to the person who values it the most (this is called Maximizing Social Surplus).
How do you get them to tell you their true value? If you just ask “How much will you pay?”, they might lie to get a better deal.
Attempt 1: The First-Price Auction¶
This is the most intuitive format.
Everyone writes a bid in a sealed envelope.
Highest bid wins.
Winner pays their bid.
The Flaw: If you value the phone at $100, you would never bid $100. If you did, your profit (utility) would be $0. You are incentivized to shade your bid (e.g., bid $80 to try and make $20 profit).
This makes the game complex. Everyone is guessing what everyone else is guessing.
Attempt 2: The Vickrey Auction (Second-Price)¶
This is the “magic” solution used in modern economics (and variations of it are used by eBay and Google Ads).
Everyone writes a bid in a sealed envelope.
Highest bid wins.
Winner pays the Second-Highest price.
The Claim: In a Second-Price auction, your best strategy is to tell the exact truth, no matter what anyone else does.
Let’s prove this with a simulation.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def run_auction(bidders, valuations, bids, auction_type='second_price'):
"""
Simulates a single-item auction.
bidders: List of names
valuations: List of true values (v_i)
bids: List of actual bids submitted (b_i)
auction_type: 'first_price' or 'second_price'
"""
# 1. Find the Winner (Highest Bid)
# We use np.argmax to find the index of the highest bid
winner_idx = np.argmax(bids)
winner_name = bidders[winner_idx]
winning_bid = bids[winner_idx]
# 2. Determine Payment
if auction_type == 'first_price':
payment = winning_bid
elif auction_type == 'second_price':
# Sort bids to find the second highest
sorted_bids = sorted(bids, reverse=True)
# The second highest is at index 1
payment = sorted_bids[1]
# 3. Calculate Utility (Profit)
# Utility = True Value - Payment (if you win)
# Utility = 0 (if you lose)
winner_true_value = valuations[winner_idx]
utility = winner_true_value - payment
return winner_name, payment, utility
# --- SIMULATION ---
# Define 5 Bidders and their TRUE valuations (unknown to the seller)
names = ['Alice', 'Bob', 'Charlie', 'Dave', 'Eve']
true_values = [100, 80, 60, 90, 40] # Alice wants it most ($100)
print(f"--- TRUE VALUATIONS (Private) ---")
for n, v in zip(names, true_values):
print(f"{n}: ${v}")
print("-" * 30)
# SCENARIO 1: First-Price Auction (Strategic Bidding)
# Everyone lies! They bid 80% of their value to try and make a profit.
bids_first_price = [v * 0.8 for v in true_values]
winner_1, pay_1, util_1 = run_auction(names, true_values, bids_first_price, 'first_price')
print(f"\n[Scenario 1: First-Price Auction]")
print(f"Bids (Strategic): {bids_first_price}")
print(f"Winner: {winner_1}")
print(f"Payment: ${pay_1:.2f}")
print(f"Winner's Profit (Utility): ${util_1:.2f}")
# SCENARIO 2: Vickrey (Second-Price) Auction (Truthful Bidding)
# Everyone tells the truth because the math says they should.
bids_second_price = true_values # Direct truth
winner_2, pay_2, util_2 = run_auction(names, true_values, bids_second_price, 'second_price')
print(f"\n[Scenario 2: Second-Price Auction]")
print(f"Bids (Truthful): {bids_second_price}")
print(f"Winner: {winner_2}")
print(f"Payment: ${pay_2:.2f} (This is the 2nd highest bid!)")
print(f"Winner's Profit (Utility): ${util_2:.2f}")
# --- VISUALIZATION ---
plt.figure(figsize=(10, 5))
# Plotting the Truthful/Second Price Scenario
bars = plt.bar(names, bids_second_price, color='skyblue', label='Bid (True Value)')
# Highlight the winner and the payment line
plt.bar(winner_2, bids_second_price[names.index(winner_2)], color='green', label='Winner')
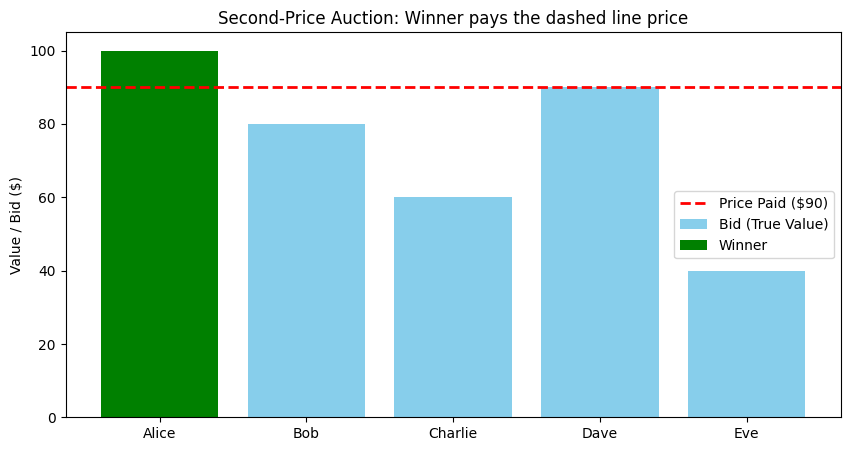
plt.axhline(y=pay_2, color='red', linestyle='--', linewidth=2, label=f'Price Paid (${pay_2})')
plt.title("Second-Price Auction: Winner pays the dashed line price")
plt.ylabel("Value / Bid ($)")
plt.legend()
plt.show()--- TRUE VALUATIONS (Private) ---
Alice: $100
Bob: $80
Charlie: $60
Dave: $90
Eve: $40
------------------------------
[Scenario 1: First-Price Auction]
Bids (Strategic): [80.0, 64.0, 48.0, 72.0, 32.0]
Winner: Alice
Payment: $80.00
Winner's Profit (Utility): $20.00
[Scenario 2: Second-Price Auction]
Bids (Truthful): [100, 80, 60, 90, 40]
Winner: Alice
Payment: $90.00 (This is the 2nd highest bid!)
Winner's Profit (Utility): $10.00
What did we learn?¶
Look at the output of Scenario 2 (Second-Price Auction).
Alice had the highest value ($100) and she won. This is Socially Optimal.
Alice bid $100, but she only paid $90 (Dave’s bid).
Alice made a profit of $10.
Why is telling the truth a Dominant Strategy? Suppose Alice tries to lie in a Second-Price Auction:
Case A (Underbid): She bids $85 instead of $100.
She still wins (since $85 > $90 is false, wait... she would LOSE!).
If she bids $85, Dave (bidding $90) would win. Alice gets $0 utility. Lying hurt her.
Case B (Overbid): She bids $150.
She still wins. She still pays the second highest price ($90).
Her utility is exactly the same. Lying didn’t help.
This leads us to the most important theorem in Mechanism Design:
Vickrey’s Theorem: In a second-price sealed-bid auction, truthful bidding is a dominant strategy. It guarantees the item goes to the person who values it most, and it is computationally easy to run.